Thank you for joining me here on Part 2 of Raman Spectroscopy and Artificial Intelligence. If you’d like to understand some of the pre-processing methods applied to a Raman spectrum before the initial stages of AI classifying, please see Part 1.
Peak Finder
PCA
Support Vector Machine
Naive Bayes
Regression
K-nearest neighbour
Random Forests
Decision Trees
Artificial Neural Networks
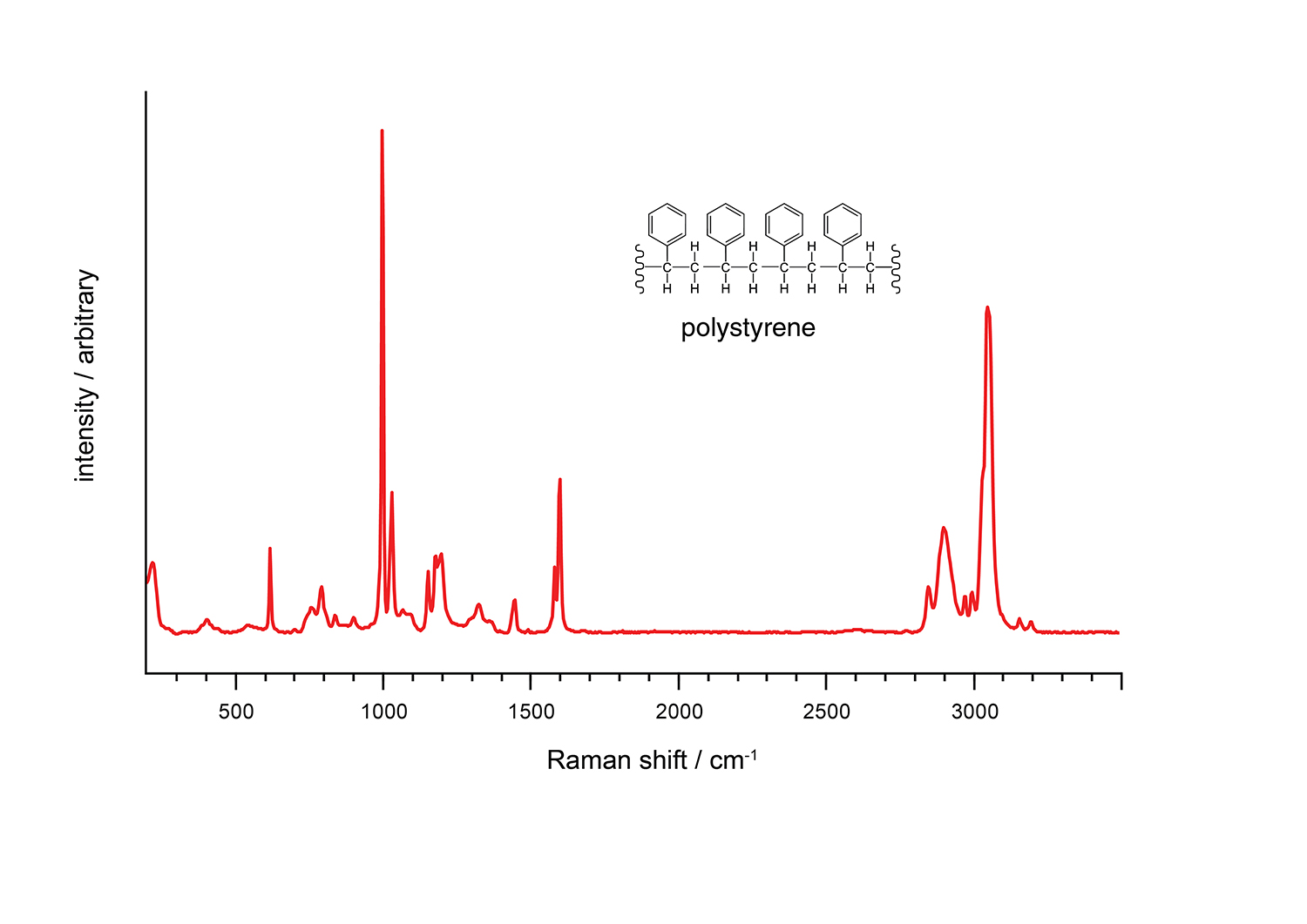
Fig 1: Raman spectrum of polystyrene
A standard Raman spectrum reveals a lot of information about the chemicals you are measuring. Firstly, just as each human being has a unique fingerprint, each chemical has a unique Raman signature and can therefore be identified by comparing it with a known spectrum. Additionally, the peaks in the spectrum of scattered light reveal the modes of vibration of the molecular bonds. Raman spectroscopy is capable of detecting vibrations of non-polar bonds within the same atom, including C-C, S-S, and N-N bonds. The observations obtained through Raman spectroscopy mainly pertain to symmetrical skeletal vibrations. Utilising the best Peak Finder algorithm is crucial to identifying these modes while different Raman systems produce different intensities.
Peak Finder
A clear, baseline-corrected and smooth Raman signal is characterised by its peaks along the range of wavelengths. Since many companies and scientists will use various types of lasers at different wavelengths, it's best to generalise the spectra based on the Raman shift. This will allow scientists to compare their spectra and — most importantly — compare the locations of the peaks.
Here's a Python script using the scipy and numpy libraries that can find peaks in data that also contains noise:
pythonCopy code
import numpy as np
from scipy.signal import find_peaks
# generate some sample data with noise
x = np.linspace(0, 10, 1000)
y = np.sin(x) + np.random.normal(0, 0.1, 1000)
# find peaks in the data using scipy.signal.find_peaks
peaks, _ = find_peaks(y, height=0.5, distance=50)
# print the peak values and their positions in the data
print("Peaks found:")
for i in range(len(peaks)):
print("Peak value:", y[peaks[i]], "at position:", x[peaks[i]])
Here, we first generate some sample data y with noise using the numpy library. Then, we use the find_peaks function from the scipy.signal library to find the peaks in the data. The height parameter specifies the minimum height of the peaks and the distance parameter specifies the minimum distance between the peaks. We then print out the peak values and their positions in the data.
You can adjust the height and distance parameters as needed for your specific dataset.
PCA
Raman spectrum analysis is a powerful tool for identifying the chemical composition of substances. However, analysing large datasets of Raman spectra can be overwhelming due to the complexity of the data. One of the challenges is understanding the relationship between Raman intensity and Raman shift. These two variables are often directly related, and blindly reducing one of them can lead to the loss of valuable information and incorrect conclusions.
To address this issue, data dimensionality reduction techniques, such as Principal Component Analysis (PCA), have become widely used in pre-processing Raman spectrum data. PCA is a powerful data dimension reduction algorithm that maps high-dimensional data to lower-dimensional space while preserving the essential features of the data. The main idea behind PCA is to find a set of mutually orthogonal coordinate axes that capture the maximum variance of the data. By selecting the k features with the largest eigenvalue, the data matrix can be transformed into a new space with fewer features. This process improves the data processing speed and reduces the complexity of the analysis.
The process of PCA involves calculating the covariance matrix of the Raman spectrum data, finding the eigenvalues and eigenvectors of the covariance matrix, and selecting the k features with the largest eigenvalue. The resulting data matrix is then transformed into a new space with fewer features, which can be easily visualized and analysed.

Fig 2: the process of PCA analysing the components of the Raman spectrum of food substances. The figure shows how the original data matrix is transformed into a new space with two principal components, which capture the maximum variance of the data. By analysing these components, it is possible to identify the chemical composition of the food substance and understand its properties.
In this Python example, we generate a signal, and process this complexity into useful PC plots.

Fig 3: Randomly generated spectrum of sinusoidal waves
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# Generate some sample sine and cosine spectra
wavelengths = np.linspace(400, 700, 100)
spectra = []
for i in range(30):
noise = np.random.random()
sine_spectrum = 0.5 * np.sin(2*np.pi*i/10 * wavelengths) + noise
cosine_spectrum = 0.5 * np.cos(2*np.pi*i/10 * wavelengths) + noise
spectra.append(sine_spectrum)
spectra.append(cosine_spectrum)
spectra = np.array(spectra)
# Plot the spectra
plt.figure()
for i in range(spectra.shape[0]):
plt.plot(wavelengths, spectra[i])
# Perform PCA
pca = PCA(n_components=2)
pca.fit(spectra)
scores = pca.transform(spectra)
# Plot the PCA scores
plt.figure()
plt.scatter(scores[:,0], scores[:,1])
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

Fig 4: the first two Principle Components of the spectrums plotted
We will now explore examples of Machine Learning tools and algorithms which will implement in classifying our datasets.
Support Vector Machine
A support vector machine (SVM) is a supervised machine learning algorithm that can be used for classification or regression tasks. The SVM algorithm tries to find the best possible boundary or hyperplane that separates different classes of data in a high-dimensional space. This boundary is chosen to maximize the margin or distance between the classes, hence the name "support vector machine".
In simpler terms, imagine you have a set of points on a 2D graph that belong to two different classes, for example, blue and red points. Your task is to draw a line or curve that separates the two classes as best as possible. A support vector machine finds the line or curve that maximizes the distance between the closest points of each class, known as support vectors. This line or curve can then be used to predict the class of new data points based on which side of the boundary they fall.

Fig 5: plotted SVM of red and blue points, and classified into two groups
This code generates 100 random points on a 2D plane and assigns them to two classes based on whether the y-coordinate is greater than the x-coordinate or not. It then fits an SVM model with a linear kernel and a regularization parameter of 1.0. Finally, it plots the data points, the decision boundary, and the support vectors.
The accuracy score of an SVM model is the proportion of correctly classified data points out of all the data points. In other words, it's the number of true positives and true negatives divided by the total number of data points.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
# Generate some random data
np.random.seed(0)
X = np.random.randn(100, 2)
y = np.where(X[:, 1] > X[:, 0], 1, -1)
# Fit the SVM model
clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y)
# Plot the data and decision boundary
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
XX, YY = np.meshgrid(xx, yy)
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
Z = Z.reshape(XX.shape)
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
print("Accuracy:", clf.score(X, y))
plt.show()
SVM is a binary classification model that uses a linear classifier to identify the most significant gap in the feature space. Its learning strategy is to maximize this gap by solving a convex quadratic programming problem. The model finds a hyperplane that can separate labelled training data from the boundary, usually by analysing data points near potential hyperplanes. SVM can handle complex classification tasks by using kernel techniques to transform nonlinear inputs into high-dimensional feature spaces. Its core objective is to maximize the classification margin by optimizing the support vector, which represents the distance between a point and the hyperplane.
Naive Bayes
Naive Bayes is a probabilistic algorithm used in machine learning for classification problems. It is based on Bayes' theorem, which states that the probability of a hypothesis H (in this case, a class label) given some observed evidence E (in this case, a set of features or attributes) is proportional to the likelihood of the evidence given the hypothesis multiplied by the prior probability of the hypothesis. Mathematically, this can be expressed as:
P(H | E) = P(E | H) \ P(H) / P(E)*
where P(H | E) is the posterior probability of H given E, P(E | H) is the likelihood of E given H, P(H) is the prior probability of H, and P(E) is the marginal probability of E.
In the case of Naive Bayes, the "naive" assumption is that the features are conditionally independent given the class label, meaning that the presence or absence of one feature does not affect the presence or absence of another feature. This allows us to simplify the likelihood calculation to a product of individual probabilities:
P(E | H) = P(e1 | H) P(e2 | H) ... \ P(en | H)*
where e1, e2, ..., en are the individual features.
To generate a Python code for a graphical analogy, we can use the following example. Suppose we have a dataset of fruits with two features: colour (red or yellow) and shape (round or oblong), and we want to classify them as either apples or bananas.
First, we need to calculate the prior probabilities of each class label based on the frequency in the dataset. Let's assume we have 10 apples and 8 bananas:
import matplotlib.pyplot as plt
import numpy as np
# prior probabilities
P_apple = 10 / 18
P_banana = 8 / 18
# likelihoods
P_red_given_apple = 8 / 10
P_yellow_given_apple = 2 / 10
P_round_given_apple = 5 / 10
P_oblong_given_apple = 5 / 10
P_yellow_given_banana = 6 / 8
P_red_given_banana = 2 / 8
P_round_given_banana = 3 / 8
P_oblong_given_banana = 5 / 8
# posterior probabilities for a new fruit with features (red, round)
P_red_round_given_apple = P_red_given_apple * P_round_given_apple
P_red_round_given_banana = P_red_given_banana * P_round_given_banana
P_apple_given_red_round = P_red_round_given_apple * P_apple / (P_red_round_given_apple * P_apple + P_red_round_given_banana * P_banana)
P_banana_given_red_round = P_red_round_given_banana * P_banana / (P_red_round_given_apple * P_apple + P_red_round_given_banana * P_banana)
# generate mesh grid for the features
x = np.linspace(0, 1, 101)
X, Y = np.meshgrid(x, x)
# calculate the likelihood of the observed features for each class
Z_apple = P_red_given_apple**X * (1 - P_red_given_apple)**(1 - X) * P_round_given_apple**Y * (1 - P_round_given_apple)**(1 - Y) * P_apple
Z_banana = P_red_given_banana**X * (1 - P_red_given_banana)**(1 - X) * P_round_given_banana**Y * (1 - P_round_given_banana)**(1 - Y) * P_banana
# plot the decision boundary
plt.contour(X, Y, Z_apple / (Z_apple + Z_banana), levels=[0.5], colors='black')
# plot the training data
banana_sizes = [30]*8
apple_sizes = [30]*10
plt.scatter([0.8]*8, [0.1, 0.15, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5], s=banana_sizes, c='yellow', label='banana')
plt.scatter([0.1]*10, [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95], s=apple_sizes, c='red', label='apple')
# plot the new fruit
plt.scatter([0.5], [0.6], s=200, c='green', label='new fruit')
# add labels and legend
plt.xlabel('color')
plt.ylabel('shape')
plt.xlim(0,1)
plt.ylim(0,1)
plt.legend()
# show the plot
plt.show()

Fig 6: differentiating two classes of groups across a hyperplane.
In the context of the code and graph analogy explanation, I provided earlier, a "new fruit" refers to a hypothetical fruit that we want to classify based on its features, which in this case are its colour and shape. We use the Naive Bayes algorithm to predict whether this new fruit is more likely to be an apple or a banana based on the observed features.
Naive Bayes classifier in machine learning uses Bayes theorem to assume feature independence and is highly scalable. It requires linearly related parameters and uses maximum likelihood estimation for training. Prior probabilities can be assumed equal or estimated from training set occurrences. The classifier assigns class labels to problem instances from a limited set, assuming label independence.
Regression
In machine learning, regression refers to the process of modelling the relationship between a dependent variable (usually denoted as 'y') and one or more independent variables (usually denoted as 'x').
The goal of regression analysis is to find a function that best describes the relationship between the variables. The most common form of regression is linear regression, where the function that describes the relationship between the variables is a straight line.
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Generate some random data
X = np.arange(1, 11).reshape((-1, 1))
y = np.array([6, 5, 9, 10, 14, 19, 17, 19, 22, 23])
# Create a linear regression object
model = LinearRegression()
# Train the model using the training sets
model.fit(X, y)
# Predict values for new data
y_pred = model.predict(X)
# Calculate the R-squared value
r2 = model.score(X, y)
# Plot the data and the fitted line
plt.scatter(X, y)
plt.plot(X, y_pred, color='red')
plt.xlabel('X')
plt.ylabel('y')
plt.title('R-squared value: {:.2f}'.format(r2))
plt.show()

Fig 7: Linear regression of points
Suppose you have collected data on the weights and prices of apples and bananas sold in a market. You want to build a regression model to predict the price of each fruit based on its weight. You have the following dataset:
| Fruit | Weight (kg) | Price (USD) |
| Apple | 0.5 | 1.5 |
| Apple | 0.75 | 2.0 |
| Apple | 1.0 | 2.5 |
| Apple | 1.25 | 3.0 |
| Apple | 1.5 | 3.5 |
| Banana | 0.25 | 0.5 |
| Banana | 0.5 | 1.0 |
| Banana | 0.75 | 1.5 |
| Banana | 1.0 | 2.0 |
| Banana | 1.25 | 2.5 |
To perform linear regression on this data, we can use the scikit-learn library in Python. Here's an example code to build a regression model to predict the price of each fruit based on its weight:
# Import necessary libraries
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Load the data into a pandas dataframe
data = pd.DataFrame({
'Fruit': ['Apple', 'Apple', 'Apple', 'Apple', 'Apple', 'Banana', 'Banana', 'Banana', 'Banana', 'Banana'],
'Weight': [0.5, 0.75, 1.0, 1.25, 1.5, 0.25, 0.5, 0.75, 1.0, 1.25],
'Price': [1.5, 2.0, 2.5, 3.0, 3.5, 0.5, 1.0, 1.5, 2.0, 2.5]
})
# Encode the fruit column as numeric values
data['Fruit'] = data['Fruit'].map({'Apple': 0, 'Banana': 1})
# Extract the features and target variable
X = data[['Fruit', 'Weight']]
y = data['Price']
# Create a linear regression object
model = LinearRegression()
# Train the model using the training sets
model.fit(X, y)
# Predict the prices for new data
new_data = pd.DataFrame({
'Fruit': ['Apple', 'Banana'],
'Weight': [1.75, 1.5]
})
new_data['Fruit'] = new_data['Fruit'].map({'Apple': 0, 'Banana': 1})
predicted_prices = model.predict(new_data)
# Print the predicted prices
print(predicted_prices)
K-nearest neighbour
K-Nearest Neighbours (KNN) is a type of supervised machine learning algorithm used for classification and regression. It is a non-parametric and instance-based algorithm that classifies a new data point based on the majority class of its K-nearest neighbours in the feature space. In other words, KNN looks for the K data points in the training set that is closest to the new data point and assigns the new data point the label of the majority class among those K neighbours.
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
# Generate some random classification data
X, y = make_classification(n_samples=300, n_features=2, n_redundant=0, random_state=42)
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create a KNN classifier object
knn = KNeighborsClassifier(n_neighbors=5)
# Train the classifier using the training data
knn.fit(X_train, y_train)
# Make predictions on the testing data
y_pred = knn.predict(X_test)
# Plot the data points with different colors for different classes
plt.scatter(X[:, 0], X[:, 1], c=y)
# Plot the decision boundary
h = 0.02
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.2)
# Show the plot
plt.show()

Fig 8: splitting two classes based on a k-nearest neighbour algorithm.
In this code, we first generate some random classification data using the make_classification function from scikit-learn. We then split the data into training and testing sets using the train_test_split function. We create a KNeighborsClassifier object with n_neighbors set to 5, which means that the algorithm will consider the 5 nearest neighbours to make predictions. We train the classifier using the fit method on the training data and then use the predict method to make predictions on the testing data. Finally, we plot the data points with different colours for different classes and plot the decision boundary using the contourf function. The decision boundary shows the region where the KNN classifier assigns a certain class to a data point.
KNN is a classification and regression method that finds K instances nearest to a new input instance in a training dataset and classifies the input into the majority class among those K neighbours. The selection of the K-value is important, as a small K may lead to overfitting while a large K may increase prediction errors. Euclidean distance is used to measure the nearest neighbour and feature normalization can prevent overfitting.
Here's another example of how we can take a PCA of plotting bananas and apples, and then take a new PC and determine its class based on the clusters we’ve plotted. The PCA is completed by PC1 saying how ‘banana-ish’ the fruit is and PC2 is saying how ‘apple-ish’ the fruit is.
import matplotlib.pyplot as plt
# Define the data
apples = [(2, 4), (3, 5), (1, 3), (5, 6), (4, 4)]
bananas = [(1, 1), (3, 2), (2, 3), (4, 1), (5, 2)]
# Define a function to calculate the Euclidean distance between two points
def euclidean_distance(point1, point2):
return ((point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2) ** 0.5
# Define the k-nearest neighbor algorithm
def knn(k, new_point):
# Calculate the distances between the new point and all the data points
distances = []
for point in apples + bananas:
distance = euclidean_distance(point, new_point)
distances.append((point, distance))
# Sort the distances from smallest to largest
sorted_distances = sorted(distances, key=lambda x: x[1])
# Get the k-nearest neighbors
k_nearest_neighbors = [x[0] for x in sorted_distances[:k]]
# Count the number of apples and bananas among the k-nearest neighbors
num_apples = sum([1 for x in k_nearest_neighbors if x in apples])
num_bananas = sum([1 for x in k_nearest_neighbors if x in bananas])
# Return the class with the most votes
if num_apples > num_bananas:
return "apple"
else:
return "banana"
# Test the algorithm with a new point
new_point = (2, 2)
print(knn(3, new_point)) # Output: "banana"
fig, ax = plt.subplots()
ax.scatter([x[0] for x in apples], [x[1] for x in apples], color='red', label='Apples')
ax.scatter([x[0] for x in bananas], [x[1] for x in bananas], color='orange', label='Bananas')
# Add labels and legend
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title('Apples and Bananas')
ax.legend()
# Add the new point
ax.scatter(new_point[0], new_point[1], color='green', label='New Point')
plt.show()

Fig 9: This graph bases the new fruit in the 'banana' cluster.
Random Forest
A Random Forest is a type of supervised machine-learning algorithm that is used for classification and regression tasks. It is an ensemble method that combines multiple decision trees to make more accurate predictions.
To explain Random Forest with a graph and plotting analogy, imagine you have a large dataset that represents a complex graph with many data points. Each data point represents a node on the graph and has a number of attributes (or features) associated with it. The goal is to predict the value of a target variable based on these attributes.
A single decision tree would try to split the dataset into smaller subgraphs based on the values of the features. However, since the graph is complex, a single decision tree might overfit the data and make inaccurate predictions on new data.
A random forest, on the other hand, builds multiple decision trees by randomly selecting subsets of features and data points to create each tree. This way, each tree is different and captures a different subset of the relationships between the features and the target variable.
When making a prediction, the random forest combines the outputs of all the individual decision trees to arrive at a final prediction. This process is like taking a poll from multiple people to get a more accurate result.

Fig 10: Random forest
For more detailed information on Random Forests, see a more detailed page with a step-by-step series for more accurate predictions: http://luisvalesilva.com/datasimple/random_forests.html
Random forest is a supervised learning method that creates a forest of independent decision trees by randomly sampling data and selecting features to avoid overfitting. Each tree ranks examples according to its selected characteristics and their predictions are merged for the final output. RF has anti-noise and stable performance but is complex and requires high computing power with more decision trees.
Decision trees
A decision tree is a graphical representation of a decision-making process that uses a tree-like model of decisions and their possible consequences. In machine learning, a decision tree is a supervised learning method that is used for classification and regression analysis.
Random forests are a type of ensemble learning method that uses multiple decision trees to make predictions. In a random forest, each decision tree is built independently using a random subset of the training data and features. The predictions of all trees are combined to obtain the final output. Random forests are more accurate and less prone to overfitting than individual decision trees.
# Creating a decision tree to differentiate between apples and bananas
# Define the characteristics that we will use to classify the fruits
characteristics = ["color", "size", "texture"]
# Create a sample dataset of fruits with their characteristics
dataset = [
{"color": "red", "size": "small", "texture": "smooth", "label": "apple"},
{"color": "yellow", "size": "large", "texture": "bumpy", "label": "banana"},
{"color": "green", "size": "medium", "texture": "rough", "label": "apple"},
{"color": "yellow", "size": "small", "texture": "smooth", "label": "banana"},
{"color": "red", "size": "large", "texture": "bumpy", "label": "apple"},
{"color": "yellow", "size": "medium", "texture": "rough", "label": "banana"},
]
# Define the function to split the dataset based on a given characteristic and value
def split_dataset(dataset, characteristic, value):
left = []
right = []
for item in dataset:
if item[characteristic] == value:
left.append(item)
else:
right.append(item)
return left, right
# Define the function to calculate the entropy of a dataset
def entropy(dataset):
from math import log2
labels = {}
for item in dataset:
label = item["label"]
if label not in labels:
labels[label] = 0
labels[label] += 1
entropy = 0
for label in labels:
probability = labels[label] / len(dataset)
entropy -= probability * log2(probability)
return entropy
# Define the function to find the best characteristic to split the dataset
def find_best_split(dataset, characteristics):
best_gain = 0
best_characteristic = None
for characteristic in characteristics:
values = set([item[characteristic] for item in dataset])
for value in values:
left, right = split_dataset(dataset, characteristic, value)
if len(left) == 0 or len(right) == 0:
continue
gain = entropy(dataset) - len(left) / len(dataset) * entropy(left) - len(right) / len(dataset) * entropy(right)
if gain > best_gain:
best_gain = gain
best_characteristic = (characteristic, value)
return best_characteristic
# Define the function to build the decision tree recursively
def build_tree(dataset, characteristics):
labels = [item["label"] for item in dataset]
if len(set(labels)) == 1:
return labels[0]
if len(characteristics) == 0:
return max(set(labels), key=labels.count)
best_characteristic = find_best_split(dataset, characteristics)
left, right = split_dataset(dataset, best_characteristic[0], best_characteristic[1])
tree = {}
tree["characteristic"] = best_characteristic[0]
tree["value"] = best_characteristic[1]
tree["left"] = build_tree(left, characteristics - set([best_characteristic[0]]))
tree["right"] = build_tree(right, characteristics - set([best_characteristic[0]]))
return tree
# Build the decision tree using the sample dataset and characteristics
tree = build_tree(dataset, set(characteristics))
# Define a function to classify a new fruit based on the decision tree
def classify_fruit(fruit, tree):
# Traverse the decision tree to find the classification of the fruit
while isinstance(tree, dict):
if fruit[tree["characteristic"]] == tree["value"]:
tree = tree["left"]
else:
tree = tree["right"]
return tree
# Test the classification function with a new fruit
new_fruit = {"color": "yellow", "size": "small", "texture": "smooth"}
classification = classify_fruit(new_fruit, tree)
print(f"The new fruit is classified as a {classification}")
A decision tree is a tree-like model that is used in supervised learning for classification or regression analysis. It is a flowchart-like structure where internal nodes represent a test on an attribute or characteristic, each branch represents the outcome of the test, and each leaf node represents a class label or a decision. Decision trees can handle both categorical and numerical data, and they are simple to understand and interpret, making them a popular choice for data analysis and modelling. Decision trees can be used as standalone models or as a building block for more complex models such as random forests.
Artificial Neural Networks
An ANN is a machine learning technique that uses interconnected neurons to process input signals and generate output signals. The neurons are organized into layers and the network structure is typically feedforward. ANN models like VGG, Google net, and ResNet have significantly improved with the development of deep learning. Training the neural network involves adjusting parameters to minimize the error between predicted and actual output results. Increasing the depth of the network reduces prediction error by extracting abstract features for better classification. However, more parameters can lead to overfitting, so attention must be paid to the network structure, hyperparameters selection, and independent data sets for model verification.

Fig 11: A basic feedforward neural network follows a workflow where a one-dimensional Raman spectrum is inputted, followed by local perception and feature extraction in the hidden layer, and decision-making in the output layer.
In an ANN, a large number of interconnected processing nodes, or "neurons," work together to learn patterns in data by adjusting the strength of connections between neurons based on the input they receive. This allows the network to make predictions, classify data, or perform other tasks based on the patterns it has learned from the input data.
ANNs can be used for a wide range of applications, including image and speech recognition, natural language processing, and predictive modelling. They have become increasingly popular in recent years due to advances in computing power and data availability.
Perhaps the hardest to visually conceptualise and implement directly into Python. To continue my journey into AI, and thus successfully implement them into my PhD, I will have to acquire new tools beyond the IDLE such as PyTorch and VSCode which has been suggested.
Wish me luck!
